Having resurrected my ideas about randomocracy last week, under the guise of 'randomonarchy', I was delighted to read this article whilst sitting on the train today:
Improbable research: Why random selection of MPs may be best
I hadn't realized that the Ancient Greeks were fans of the randomocratic system, and was blissfully unaware they used a device called a kleroterion to elect many of their public officials.
As a consequence, according to a most informative article by Julian Dibbell, "every [Athenian] citizen could be expected at some point in his life to be called up for a year of service." This is pretty much exactly as I'd like it: all the electorate of a country being directly involved in its governance.
To examine this from a modern perspective, Alessandro Pluchino and colleagues from the Università di Catania examined the efficiency of a parliament in which none, some, or all of the legislators were elected at random, rather than through standard party democracy.
Pluchino et al. had already shown that random promotions improved business efficiency, winning the 2010 Ig Nobel Prize for Management as a consequence.
In this new paper, they looked at the efficiency of decision-making in a parliament of two parties, or two coalitions, and variable numbers of random independent legislators. Perhaps as expected, they show that when there are no independent voices, the parliament is inefficient.
Disappointingly, at least from my 'pure randomocracy' approach, they show that the parliament is just as inefficient when 100% random. Indeed, they state that 'no particular benefit stems from abolishing Parties altogether.'
Lots of variables need to be considered, but, in summary, the study shows that there is often an optimal number of independent MPs. Even better, it provides an equation of optimal randomocracy (my term, not theirs) for a given size (p, percentage) of majority party in a parliament of N legislators:
What do you mean you don't understand it? Read the blinking paper! This stuff is important!
Anyhow, I haven't yet used the equation to calculate how randomocratic the UK parliament needs to be for it to become efficient. However, I am pretty darned certain that the N(ind) value will not be just four, as it is at present: George Galloway, Lady Hermon, Naomi Long, and Caroline Lucas.
With science on its side, let the randomocratic revolution begin!
Improbable research: Why random selection of MPs may be best
I hadn't realized that the Ancient Greeks were fans of the randomocratic system, and was blissfully unaware they used a device called a kleroterion to elect many of their public officials.
 |
| A kleroterion from the Agora Museum, Athens |
As a consequence, according to a most informative article by Julian Dibbell, "every [Athenian] citizen could be expected at some point in his life to be called up for a year of service." This is pretty much exactly as I'd like it: all the electorate of a country being directly involved in its governance.
To examine this from a modern perspective, Alessandro Pluchino and colleagues from the Università di Catania examined the efficiency of a parliament in which none, some, or all of the legislators were elected at random, rather than through standard party democracy.
Pluchino et al. had already shown that random promotions improved business efficiency, winning the 2010 Ig Nobel Prize for Management as a consequence.
In this new paper, they looked at the efficiency of decision-making in a parliament of two parties, or two coalitions, and variable numbers of random independent legislators. Perhaps as expected, they show that when there are no independent voices, the parliament is inefficient.
Disappointingly, at least from my 'pure randomocracy' approach, they show that the parliament is just as inefficient when 100% random. Indeed, they state that 'no particular benefit stems from abolishing Parties altogether.'
Lots of variables need to be considered, but, in summary, the study shows that there is often an optimal number of independent MPs. Even better, it provides an equation of optimal randomocracy (my term, not theirs) for a given size (p, percentage) of majority party in a parliament of N legislators:
What do you mean you don't understand it? Read the blinking paper! This stuff is important!
Anyhow, I haven't yet used the equation to calculate how randomocratic the UK parliament needs to be for it to become efficient. However, I am pretty darned certain that the N(ind) value will not be just four, as it is at present: George Galloway, Lady Hermon, Naomi Long, and Caroline Lucas.
 |
| Politics: it's not a lottery, but it should be. |
With science on its side, let the randomocratic revolution begin!
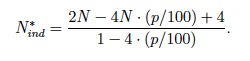
Comments